Calcul d'un Système de Drainage Périphérique
Contexte : Le drainage périphériqueDispositif de collecte et d'évacuation des eaux de ruissellement et d'infiltration autour des fondations d'un bâtiment pour protéger les murs enterrés de l'humidité..
La pérennité d'un ouvrage dépend en grande partie de la bonne gestion de l'eau à proximité de ses fondations. Un drainage périphérique efficace est essentiel pour prévenir les infiltrations, l'humidité dans les sous-sols et les désordres structurels qui peuvent en découler. Cet exercice se base sur le cas d'une maison individuelle et vise à quantifier les matériaux et à définir les caractéristiques techniques du système de drainage, conformément aux règles de l'art et au DTU 20.1Document Technique Unifié qui régit les travaux de parois et murs en maçonnerie de petits éléments. Il contient les spécifications pour la protection des murs contre les remontées capillaires et les infiltrations..
Remarque Pédagogique : Cet exercice vous apprendra à réaliser un métré complet pour un ouvrage de drainage, à calculer les volumes de terrassement et de matériaux, et à appliquer une pente pour assurer le bon écoulement des eaux.
Objectifs Pédagogiques
- Comprendre le rôle et la composition d'un drainage périphérique.
- Calculer le volume de déblai pour la tranchée drainante.
- Déterminer les quantités de matériaux nécessaires (gravier, géotextile).
- Calculer la pente du drain et les cotes altimétriques associées.
- Appliquer les recommandations du DTU 20.1.
Données de l'étude
Dimensions du Bâtiment
| Caractéristique | Valeur |
|---|---|
| Longueur extérieureLa plus grande dimension du bâtiment, mesurée sur ses faces extérieures. | 12,00 m |
| Largeur extérieureLa plus petite dimension du bâtiment, mesurée sur ses faces extérieures. | 8,00 m |
| Profondeur des fondations | -1,20 m par rapport au terrain naturel |
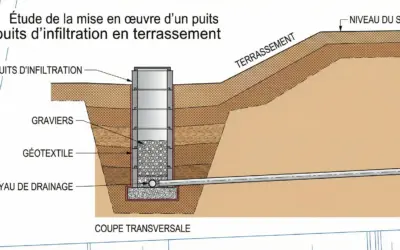
Coupe transversale du système de drainage
| Paramètre de Conception | Description | Valeur | Unité |
|---|---|---|---|
| Largeur de la tranchée | Standard pour intervention | 0,50 | m |
| Hauteur de gravier | Enrobage du drain + couche supérieure | 0,40 | m |
| Pente du drain | Conforme au DTU 20.1 | 5 | mm/m |
Questions à traiter
- Calculer le périmètre extérieur des fondations à drainer.
- Calculer le volume total de la tranchée à creuser (volume de déblai).
- Calculer le volume de gravier (granulométrie 20/40) nécessaire.
- Déterminer la surface de géotextile anti-contaminant à prévoir.
- Calculer la cote altimétrique du point le plus bas du drain, en considérant le point de départ (point haut) au ras de la semelle.
Les bases du drainage et des terrassements
Pour réaliser cet exercice, quelques notions de base en métré et en technologie du bâtiment sont nécessaires. Il s'agit principalement de calculs géométriques simples et de la compréhension du rôle de chaque composant.
1. Rôle et composition d'un drainage
Un drainage périphérique est une tranchée remplie de matériaux drainants au pied des murs enterrés. Il se compose de :
- Un drain (tuyau perforé) qui collecte l'eau.
- Du gravier propre qui constitue le massif drainant et protège le drain.
- Un géotextile qui enveloppe le gravier pour empêcher la terre de le colmater.
2. Calculs de base
Les calculs de métré reposent sur des formules géométriques simples :
- Périmètre d'un rectangle : \( P = 2 \times (L + l) \)
- Volume d'un prisme (tranchée) : \( V = \text{Longueur} \times \text{largeur} \times \text{hauteur} \)
- Pente : \( \text{Pente (en m/m)} = \frac{\text{Dénivelé (en m)}}{\text{Longueur (en m)}} \)
Correction : Calcul d'un Système de Drainage Périphérique
Question 1 : Calculer le périmètre extérieur des fondations à drainer.
Principe (le concept physique)
Le drainage fait le tour complet du bâtiment pour intercepter les eaux sur toutes ses faces. Sa longueur totale correspond donc au périmètre extérieur des murs de fondation, qui représente la ligne centrale de la future tranchée.
Mini-Cours (approfondissement théorique)
En géométrie, le périmètre est la mesure de la longueur du contour d'une figure. Dans le BTP, le calcul du périmètre est l'une des opérations de "métré" les plus fondamentales. Il permet de quantifier tous les ouvrages linéaires : longueur de fondations, de murs, de canalisations, de plinthes, etc. Maîtriser ce calcul simple est la base de toute estimation de quantité.
Remarque Pédagogique (le conseil du professeur)
Avant tout calcul, visualisez le problème. Imaginez que vous déroulez un mètre ruban tout autour de la maison. C'est cette longueur que vous cherchez. Ne confondez jamais le périmètre (une longueur, en mètres) avec la surface (une aire, en mètres carrés).
Normes (la référence réglementaire)
Il n'y a pas de "norme" pour calculer un périmètre, c'est une règle mathématique universelle. Cependant, les règles du métré dans le bâtiment exigent de bien définir s'il s'agit d'un périmètre intérieur, extérieur ou "dans l'axe". Ici, comme le drainage est à l'extérieur, on prend logiquement le périmètre extérieur.
Formule(s) (l'outil mathématique)
Formule du périmètre d'un rectangle
Hypothèses (le cadre du calcul)
Pour ce calcul, nous posons les hypothèses suivantes :
- Le bâtiment est un rectangle parfait, sans décrochement ni partie arrondie.
- Les dimensions fournies sont bien les dimensions extérieures finies du soubassement.
Donnée(s) (les chiffres d'entrée)
Les données nécessaires sont :
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Longueur | L | 12,00 | \(\text{m}\) |
| Largeur | l | 8,00 | \(\text{m}\) |
Astuces (Pour aller plus vite)
Pour un calcul mental rapide sur le chantier, vous pouvez simplement additionner la longueur et la largeur (12 + 8 = 20) puis multiplier le résultat par deux (20 x 2 = 40). C'est plus rapide que de faire (2 x 12) + (2 x 8).
Schéma (Avant les calculs)
Vue en plan du bâtiment
Calcul(s) (l'application numérique)
Calcul du périmètre
Schéma (Après les calculs)
Représentation du périmètre
Réflexions (l'interprétation du résultat)
Le résultat de 40,00 m n'est pas juste un chiffre. Il représente une longueur concrète : 40 mètres de tranchée à creuser, 40 mètres de tuyau de drain à poser, 40 mètres de matériaux à mettre en œuvre. C'est la donnée de base pour tous les calculs suivants.
Points de vigilance (les erreurs à éviter)
L'erreur la plus commune est de ne prendre qu'une seule fois la longueur et la largeur (12 + 8 = 20 m), oubliant ainsi la moitié du périmètre ! Assurez-vous de bien faire le tour complet du bâtiment.
Points à retenir (permettre a l'apprenant de maitriser la question)
Pour maîtriser cette question, retenez :
- Concept Clé : Le périmètre est le contour.
- Formule Essentielle : \(P = 2 \times (L+l)\) pour un rectangle.
- Application : C'est la longueur de base pour tous les ouvrages linéaires qui entourent une structure.
Le saviez-vous ? (la culture de l'ingénieur)
Le mot "périmètre" vient du grec ancien. "Peri" signifie "autour" et "metron" signifie "mesure". C'est littéralement "la mesure du tour". Cette étymologie simple aide à se rappeler le concept fondamental.
FAQ (pour lever les doutes)
Voici quelques questions fréquentes.
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Quel serait le périmètre pour une maison de 15 m par 10 m ?
Question 2 : Calculer le volume de déblai de la tranchée
Principe (le concept physique)
Le volume de terre à excaver (le "déblai") correspond au volume géométrique de la tranchée. On peut assimiler la tranchée à un prisme droit dont la base est la section rectangulaire (largeur × profondeur) et la hauteur est le périmètre du bâtiment.
Mini-Cours (approfondissement théorique)
Le calcul de volumes est essentiel en terrassement pour quantifier les mouvements de terre. Un "déblai" est un volume de terre retiré, tandis qu'un "remblai" est un volume de terre ajouté. Le volume d'un prisme droit (forme de notre tranchée déroulée) est toujours calculé par la formule : \( V = \text{Surface de la base} \times \text{Hauteur} \). Dans notre cas, la "hauteur" du prisme est la longueur de la tranchée.
Remarque Pédagogique (le conseil du professeur)
Pour ne pas vous tromper, raisonnez toujours en trois dimensions. Vous avez une longueur (le périmètre), une largeur et une profondeur. Le produit des trois vous donnera un volume. Assurez-vous que toutes vos unités sont en mètres pour obtenir un résultat en mètres cubes (\(\text{m}^3\)).
Normes (la référence réglementaire)
Le DTU 20.1 ne fixe pas la largeur de la tranchée, mais elle doit être suffisante pour permettre une mise en œuvre correcte (en général 40 à 50 cm). La profondeur est dictée par la nécessité de poser le drain sous le niveau de la fondation pour capter l'eau avant qu'elle n'atteigne la structure.
Formule(s) (l'outil mathématique)
Formule du volume de déblai
Hypothèses (le cadre du calcul)
Nous supposons que la profondeur et la largeur de la tranchée sont constantes sur tout le périmètre, et que les parois de la tranchée sont parfaitement verticales.
Donnée(s) (les chiffres d'entrée)
Les données nécessaires sont :
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Périmètre | P | 40,00 | \(\text{m}\) |
| Largeur tranchée | \(l_{\text{t}}\) | 0,50 | \(\text{m}\) |
| Profondeur tranchée | \(h_{\text{t}}\) | 1,20 | \(\text{m}\) |
Astuces (Pour aller plus vite)
Calculez d'abord la surface de la section de la tranchée (0,50 m × 1,20 m = 0,60 m²). Cette valeur représente le volume de déblai pour 1 mètre linéaire de tranchée. Il suffit ensuite de multiplier ce chiffre par la longueur totale (0,60 m²/ml × 40 ml = 24 m³).
Schéma (Avant les calculs)
Volume de la tranchée
Calcul(s) (l'application numérique)
Calcul du volume de déblai
Schéma (Après les calculs)
Visualisation du volume de déblai
Réflexions (l'interprétation du résultat)
24 m³ représente un volume de terre conséquent. Sur un chantier, cela se traduit par un certain nombre de rotations de camions pour évacuer les terres excédentaires, ou par la nécessité de stocker ce volume sur site s'il est réutilisé en remblai.
Points de vigilance (les erreurs à éviter)
En conditions réelles, il faut prévoir un foisonnement des terres. Un sol excavé occupe un volume plus important que dans son état compact. Pour des argiles, ce coefficient peut être de 1,25 à 1,35. Le volume à évacuer serait donc plus grand (ex: 24 m³ × 1,30 = 31,2 m³).
Points à retenir (permettre a l'apprenant de maitriser la question)
- Concept Clé : Volume = Longueur × Largeur × Profondeur.
- Application : Le volume de déblai est crucial pour estimer le coût et la durée du terrassement.
- Vigilance : Penser au foisonnement pour l'évacuation.
Le saviez-vous ? (la culture de l'ingénieur)
La gestion des déblais est un enjeu majeur sur les chantiers modernes. La terre n'est plus considérée comme un déchet mais comme une ressource. Des plateformes spécialisées (comme "Terres-en-ville") organisent le réemploi des terres de déblai d'un chantier à l'autre pour limiter le transport et la mise en décharge.
FAQ (pour lever les doutes)
Voici quelques questions fréquentes.
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Quel serait le volume de déblai si la tranchée faisait 0,60 m de large ?
Question 3 : Calculer le volume de gravier nécessaire
Principe (le concept physique)
Le volume de gravier correspond au volume de la tranchée qui sera rempli par ce matériau drainant. Ce volume est calculé de la même manière que le volume de déblai, mais en utilisant la hauteur de la couche de gravier spécifiée au lieu de la profondeur totale de la tranchée.
Mini-Cours (approfondissement théorique)
Le massif drainant en gravier a un double rôle : il constitue un milieu très perméable où l'eau peut circuler facilement vers le drain, et il sert de "squelette" qui maintient la tranchée ouverte sans se tasser. La granulométrie (ex: 20/40 mm) est choisie pour avoir un pourcentage de vides élevé, garantissant une excellente perméabilité.
Remarque Pédagogique (le conseil du professeur)
Faites bien attention à la hauteur à utiliser dans votre calcul. On ne remplit pas toute la tranchée avec du gravier, seulement une partie. Le reste sera comblé avec de la terre. Lisez attentivement l'énoncé pour identifier la bonne hauteur.
Normes (la référence réglementaire)
Le DTU 20.1 impose un enrobage complet du drain avec des matériaux granulaires. La hauteur de 40 cm spécifiée ici est une valeur courante qui permet un bon enrobage (environ 15-20 cm au-dessus du drain) tout en créant une couche drainante efficace.
Formule(s) (l'outil mathématique)
Formule du volume de gravier
Hypothèses (le cadre du calcul)
On suppose que la hauteur de la couche de gravier est constante sur toute la longueur du drainage.
Donnée(s) (les chiffres d'entrée)
Les données nécessaires sont :
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Périmètre | P | 40,00 | \(\text{m}\) |
| Largeur tranchée | \(l_{\text{t}}\) | 0,50 | \(\text{m}\) |
| Hauteur gravier | \(h_{\text{g}}\) | 0,40 | \(\text{m}\) |
Astuces (Pour aller plus vite)
Les fournisseurs de matériaux vendent souvent au poids (tonnes) et non au volume. Il faudra convertir les m³ en tonnes en utilisant la masse volumique du gravier (environ 1,6 t/m³). Pour cet exercice, il faudrait commander : 8 m³ × 1,6 t/m³ = 12,8 tonnes. Arrondissez toujours à la tonne supérieure lors de la commande.
Schéma (Avant les calculs)
Section de la tranchée à remplir de gravier
Calcul(s) (l'application numérique)
Calcul du volume de gravier
Schéma (Après les calculs)
Visualisation du volume de gravier
Réflexions (l'interprétation du résultat)
8 m³ de gravier représente un volume important à approvisionner sur le chantier. Ce calcul est essentiel pour passer la commande au fournisseur et planifier la livraison. Une erreur sur ce volume peut entraîner des coûts supplémentaires ou des retards sur le chantier.
Points de vigilance (les erreurs à éviter)
Ne pas oublier de commander un peu plus de matériaux que le volume théorique calculé (environ 5% à 10% en plus) pour compenser les imprécisions de terrassement, le tassement et les pertes sur le chantier.
Points à retenir (permettre a l'apprenant de maitriser la question)
- Concept Clé : Le volume de matériaux est lié à la géométrie de l'ouvrage qu'ils remplissent.
- Application : Ce calcul est la base de toute commande de matériaux granulaires (sable, gravier, grave...).
- Conversion : Penser à convertir les m³ en tonnes pour la commande.
Le saviez-vous ? (la culture de l'ingénieur)
Les granulats (sables, graviers) sont la deuxième ressource la plus consommée au monde après l'eau ! La recherche de solutions alternatives, comme les granulats recyclés issus de la démolition de bâtiments, est un enjeu environnemental majeur pour le secteur de la construction.
FAQ (pour lever les doutes)
Voici quelques questions fréquentes.
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Quel serait le volume de gravier si la couche devait faire 0,50 m de haut ?
Question 4 : Déterminer la surface de géotextile
Principe (le concept physique)
Le géotextile est une "toile" qui enveloppe le massif de gravier. Pour calculer sa surface, on "déroule" virtuellement le profil de la tranchée (le fond + les deux côtés) pour obtenir une largeur développée, que l'on multiplie ensuite par la longueur totale de la tranchée.
Mini-Cours (approfondissement théorique)
Le géotextile est un non-tissé. Sa fonction ici est double : filtration et séparation. Il laisse passer l'eau (filtration) mais empêche les particules fines de terre de migrer dans le gravier et de le colmater (séparation), ce qui garantit la pérennité de la capacité drainante du système.
Remarque Pédagogique (le conseil du professeur)
Imaginez que vous devez tapisser l'intérieur d'une boîte sans couvercle avec du papier cadeau. La surface de papier nécessaire est la surface du fond plus celle des quatre côtés. Ici, c'est la même logique, mais pour une tranchée très longue : on tapisse le fond et les deux parois latérales.
Normes (la référence réglementaire)
Le DTU 20.1 et les règles de l'art imposent l'utilisation d'un géotextile pour protéger le massif drainant de la contamination par les terres environnantes, surtout en sol argileux ou limoneux.
Formule(s) (l'outil mathématique)
Formule de la largeur développée
Formule de la surface du géotextile
Hypothèses (le cadre du calcul)
On suppose que le géotextile tapisse toute la hauteur des parois de la tranchée, sans prendre en compte le rabat supérieur pour l'instant.
Donnée(s) (les chiffres d'entrée)
Les données nécessaires sont :
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Périmètre | P | 40,00 | \(\text{m}\) |
| Largeur tranchée | \(l_{\text{t}}\) | 0,50 | \(\text{m}\) |
| Profondeur tranchée | \(h_{\text{t}}\) | 1,20 | \(\text{m}\) |
Astuces (Pour aller plus vite)
Les géotextiles sont vendus en rouleaux de largeurs standards (1m, 2m, 3m...). Après avoir calculé la largeur développée (ici 2,90 m), choisissez le rouleau de largeur immédiatement supérieure (ici, 3m). La surface à commander sera alors : Longueur (40m) × Largeur du rouleau (3m) = 120 m².
Schéma (Avant les calculs)
Largeur développée du géotextile
Calcul(s) (l'application numérique)
Étape 1 : Calcul de la largeur développée
Étape 2 : Calcul de la surface totale
Schéma (Après les calculs)
Surface de géotextile à plat
Réflexions (l'interprétation du résultat)
Une surface de 116 m² correspond, par exemple, à un peu moins de la moitié d'un terrain de tennis. Ce chiffre permet de choisir le conditionnement des rouleaux de géotextile et d'estimer le coût de fourniture.
Points de vigilance (les erreurs à éviter)
Il faut toujours prévoir une marge pour les recouvrements entre les laizes de géotextile (environ 20-30 cm) et pour le rabat en haut de la tranchée. Une majoration de 10% à 15% de la surface calculée est une bonne pratique. Ici : 116 × 1,10 ≈ 128 m².
Points à retenir (permettre a l'apprenant de maitriser la question)
- Concept Clé : Le calcul de surface d'un ouvrage complexe se ramène à "déplier" sa forme pour obtenir une surface plane.
- Formule : \(S = L \times \text{Largeur}_{\text{dév}}\).
- Vigilance : Penser aux recouvrements et aux pertes lors de la commande.
Le saviez-vous ? (la culture de l'ingénieur)
Les géotextiles ne sont pas seulement utilisés en drainage. On les retrouve dans de nombreux ouvrages de génie civil : sous les routes et voies ferrées pour renforcer le sol, dans la construction de digues, ou pour la protection des berges contre l'érosion.
FAQ (pour lever les doutes)
Voici quelques questions fréquentes.
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Quelle serait la surface nécessaire si la tranchée faisait 1,50 m de profondeur ?
Question 5 : Calculer la cote altimétrique du point bas
Principe (le concept physique)
L'eau ne s'écoule que par gravité, du haut vers le bas. Pour qu'un drain fonctionne, il doit donc avoir une pente continue. On définit un point de départ (point haut) et on calcule la descente totale (dénivelé) jusqu'au point d'arrivée (point bas) en fonction de la pente et de la longueur.
Mini-Cours (approfondissement théorique)
L'altimétrie est la partie de la topographie qui traite de la mesure des altitudes. Sur un chantier, on travaille avec des "cotes" par rapport à un point de référence (le "zéro" du projet). Une cote négative signifie qu'on est en dessous de ce point de référence. Une pente de 5 mm/m signifie que pour chaque mètre parcouru horizontalement, on descend de 5 millimètres verticalement.
Remarque Pédagogique (le conseil du professeur)
Attention aux unités ! La pente est souvent donnée en mm/m ou en %. Pour les calculs, il est plus sûr de tout convertir en m/m. Rappelez-vous que 1% = 1 cm/m = 10 mm/m = 0,01 m/m. Ici, 5 mm/m = 0,5% = 0,005 m/m.
Normes (la référence réglementaire)
Le DTU 20.1 préconise une pente comprise entre 3 et 10 mm/m. Une pente trop faible (< 3 mm/m) risque de ne pas être suffisante pour un bon écoulement et pourrait s'annuler avec les imprécisions de pose. Une pente trop forte (> 10 mm/m) n'est pas nécessaire et peut créer une tranchée très profonde à l'arrivée.
Formule(s) (l'outil mathématique)
Formule du dénivelé
Formule de la cote du point bas
Hypothèses (le cadre du calcul)
On suppose que le point haut du fil d'eau du drain coïncide avec le bas de la semelle de fondation, soit la cote -1,20 m, et que la pente est appliquée de manière constante sur les 40 mètres de périmètre.
Donnée(s) (les chiffres d'entrée)
Les données nécessaires sont :
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Longueur du drain | P | 40,00 | \(\text{m}\) |
| Pente | p | 5 (soit 0,005) | \(\text{mm/m}\) (\(\text{m/m}\)) |
| Cote point haut | \(Z_{\text{haut}}\) | -1,20 | \(\text{m}\) |
Astuces (Pour aller plus vite)
Pour vérifier votre calcul, la pente de 5 mm/m correspond à une descente de 5 cm pour 10 m. Comme notre drain fait 40 m (4 x 10 m), la descente totale sera de 4 x 5 cm = 20 cm. C'est une vérification mentale simple et efficace.
Schéma (Avant les calculs)
Profil en long du drain
Calcul(s) (l'application numérique)
Étape 1 : Calcul du dénivelé total
Étape 2 : Calcul de la cote du point bas
Schéma (Après les calculs)
Profil en long avec cotes
Réflexions (l'interprétation du résultat)
Le point le plus bas du drain se trouvera 20 cm plus bas que le point le plus haut, soit à -1,40 m. Cette information est cruciale pour le terrassier qui réalisera la tranchée. Il utilisera un niveau laser pour s'assurer que le fond de la tranchée respecte bien cette pente tout le long du parcours.
Points de vigilance (les erreurs à éviter)
La principale erreur est de se tromper dans le signe : on descend, donc on soustrait le dénivelé. La cote du point bas doit être plus négative que celle du point haut. Une erreur d'unité sur la pente (utiliser 5 au lieu de 0,005) est également fatale et donnerait un résultat absurde.
Points à retenir (permettre a l'apprenant de maitriser la question)
- Concept Clé : La gravité nécessite une pente pour l'écoulement.
- Formule : Dénivelé = Pente × Longueur.
- Conversion : Toujours convertir la pente en m/m pour les calculs de dénivelé en mètres.
Le saviez-vous ? (la culture de l'ingénieur)
Les Romains étaient des maîtres absolus dans la gestion des pentes. Leurs aqueducs, comme le Pont du Gard, acheminaient l'eau sur des dizaines de kilomètres avec des pentes extrêmement faibles et précises (parfois de l'ordre de 25 cm par kilomètre, soit 0,25 mm/m !), une prouesse technique remarquable pour l'époque.
FAQ (pour lever les doutes)
Voici quelques questions fréquentes.
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Quelle serait la cote du point bas avec une pente de 1% (soit 10 mm/m) ?
Outil Interactif : Simulateur de Terrassement
Utilisez les curseurs pour modifier les dimensions de la maison et observez l'impact direct sur les volumes de matériaux nécessaires. Les calculs se basent sur les hypothèses de l'exercice (tranchée de 0,50m de large et 1,20m de profondeur, couche de gravier de 0,40m).
Paramètres du Bâtiment
Métré Estimatif
Quiz Final : Testez vos connaissances
1. Quelle est la pente minimale recommandée pour un drain par le DTU 20.1 ?
2. Quel est le rôle principal du géotextile dans un système de drainage ?
3. En règle générale, où doit être positionné le dessus du drain ?
4. Dans un calcul de métré, 1 m³ équivaut à :
5. Pourquoi le gravier utilisé doit-il être propre et de granulométrie contrôlée (ex: 20/40) ?
Glossaire
- Drainage périphérique
- Dispositif de collecte et d'évacuation des eaux de ruissellement et d'infiltration autour des fondations d'un bâtiment pour protéger les murs enterrés de l'humidité.
- DTU 20.1
- Document Technique Unifié qui régit les travaux de parois et murs en maçonnerie de petits éléments. Il contient les spécifications pour la protection des murs contre les remontées capillaires et les infiltrations.
- Géotextile
- Feutre synthétique perméable, utilisé pour séparer des matériaux de granulométries différentes (ici, la terre et le gravier) et pour filtrer l'eau tout en retenant les particules fines.
- Altimétrie
- Mesure des altitudes ou des "cotes" par rapport à un niveau de référence (souvent le niveau de la mer, ou un point de référence local sur un chantier).
- Foisonnement
- Augmentation du volume apparent d'un sol lorsqu'il est extrait de son état compact. Ce phénomène doit être pris en compte pour le calcul des volumes de terre à évacuer par camion.
D’autres exercices de Travaux annexes:





0 commentaires