Calcul du Tassement d'un Remblai sur Sol Compressible

Contexte : Le Tassement des solsAffaissement vertical d'un sol sous l'effet d'une charge, dû notamment à l'expulsion de l'eau (consolidation)..

Nous étudions la construction d'un remblai routier sur une couche d'argile molle saturée. L'ajout de cette charge va provoquer un affaissement du sol sous-jacent, appelé tassement. Il est crucial de prédire l'amplitude de ce tassement (\(S_f\)) pour garantir la viabilité à long terme de l'ouvrage (route, bâtiment, etc.). Cet exercice se concentre sur le calcul du tassement final en utilisant la théorie de la consolidation unidimensionnelle de Terzaghi.

Remarque Pédagogique : Cet exercice vous apprendra à appliquer la théorie de la consolidation pour estimer le tassement final d'une couche de sol compressible sous un chargement uniforme, un calcul fondamental en géotechnique et en terrassement.

Objectifs Pédagogiques

Identifier les paramètres de sol pertinents (indice des vides, indice de compression).
Calculer la contrainte effective initiale (\( \sigma'_{\text{v0}} \)) et la contrainte additionnelle (\( \Delta\sigma' \)).
Appliquer la formule du tassement oedométrique pour un sol normalement consolidé.
Comprendre l'impact du tassement sur un ouvrage et les ordres de grandeur.

Données de l'étude : Remblai sur Argile

Un remblai routier de 8,0 m de hauteur doit être construit sur un terrain naturel. Le profil de sol est constitué d'une couche d'argile molle saturée de 10,0 m d'épaisseur, reposant sur un substratum rocheux considéré comme rigide et imperméable. La nappe phréatique est à la surface du terrain naturel.

Fiche Technique

Caractéristique	Valeur
Hauteur du remblai (\(H_{\text{remb}}\))	8,0 m
Poids volumique du remblai (\(\gamma_{\text{remb}}\))	20 kN/m³
Épaisseur couche d'argile (\(H_{\text{sol}}\))	10,0 m
Poids volumique saturé argile (\(\gamma_{\text{sat}}\))	18 kN/m³
Poids volumique de l'eau (\(\gamma_{w}\))	10 kN/m³ (simplifié)
Indice des vides initial (\(e_0\))	1,20
Indice de compression (\(C_c\))	0,45
État du sol	Normalement consolidé

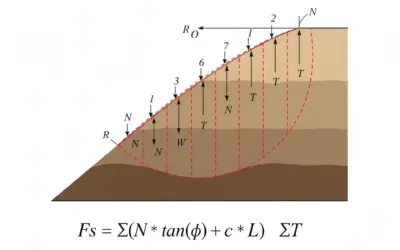
Schéma du Remblai sur Sol Compressible

Paramètre	Symbole	Valeur	Unité
Hauteur remblai	\(H_{\text{remb}}\)	8.0	m
Poids volumique remblai	\(\gamma_{\text{remb}}\)	20	kN/m³
Épaisseur argile	\(H_{\text{sol}}\)	10.0	m
Poids volumique saturé	\(\gamma_{\text{sat}}\)	18	kN/m³
Indice des vides initial	\(e_0\)	1,20	-
Indice de compression	\(C_c\)	0,45	-

Questions à traiter

Calculer la contrainte verticale totale (\( \sigma_v \)), la pression interstitielle (\( u_0 \)), et la contrainte effective initiale (\( \sigma'_{\text{v0}} \)) au milieu de la couche d'argile (à 5m de profondeur) avant la construction du remblai.
Calculer la contrainte verticale additionnelle (\( \Delta\sigma' \)) induite par le remblai. On la supposera constante sur toute la hauteur de la couche d'argile.
Calculer la contrainte effective finale (\( \sigma'_{\text{vf}} \)) au milieu de la couche d'argile après consolidation complète.
Estimer le tassement de consolidation primaire total (\( S_f \)) de la couche d'argile.
Le tassement calculé vous semble-t-il acceptable pour une route ? Discutez brièvement des solutions techniques qui pourraient être envisagées si ce tassement est jugé excessif.

Les bases du Tassement par Consolidation

Le tassement d'un sol fin saturé (comme l'argile) sous une charge est principalement dû à l'expulsion lente de l'eau contenue dans ses pores. Ce phénomène est appelé consolidation. Le calcul de ce tassement repose sur le principe de la contrainte effective de Terzaghi.

1. Principe de la Contrainte Effective (Terzaghi)
La contrainte totale (\(\sigma\)) en un point du sol se décompose en deux parties : la pression de l'eau interstitielle (\(u\)) et la contrainte effective (\(\sigma'\)), qui est la contrainte supportée par le squelette solide du sol. \[ \sigma' = \sigma - u \] C'est la variation de la contrainte effective (\(\Delta\sigma'\)) qui provoque le tassement, et non la contrainte totale.

2. Tassement Oedométrique (Sol Normalement Consolidé)
Pour un sol dit "normalement consolidé" (qui n'a jamais supporté plus de charge que sa charge actuelle), le tassement final (\(S_f\)) est calculé avec la formule logarithmique suivante : \[ S_f = \frac{C_c}{1 + e_0} \cdot H_{\text{sol}} \cdot \log_{10} \left( \frac{\sigma'_{\text{vf}}}{\sigma'_{\text{v0}}} \right) \] Où :

\(C_c\) est l'indice de compression (mesure la compressibilité).
\(e_0\) est l'indice des vides initial.
\(H_{\text{sol}}\) est l'épaisseur de la couche compressible.
\(\sigma'_{\text{v0}}\) est la contrainte effective verticale initiale.
\(\sigma'_{\text{vf}}\) est la contrainte effective verticale finale (\(\sigma'_{\text{v0}} + \Delta\sigma'\)).

Correction : Calcul du Tassement d'un Remblai sur Sol Compressible

Question 1 : Calculer la contrainte effective initiale (\( \sigma'_{\text{v0}} \))

Principe

Nous devons calculer les contraintes au milieu de la couche d'argile, soit à une profondeur de \( z = 5 \, \text{m} \) sous la surface du sol d'origine. La contrainte effective est la contrainte totale moins la pression de l'eau.

Mini-Cours

La contrainte verticale totale en un point \(z\) sous la surface est le poids de la colonne de sol au-dessus de ce point. La pression interstitielle hydrostatique est la pression de l'eau à cette profondeur.

Remarque Pédagogique

Il est souvent plus simple de calculer directement la contrainte effective en utilisant le poids volumique déjaugé \(\gamma'\) pour la partie du sol sous la nappe phréatique.

Normes

Les définitions des contraintes totales, interstitielles et effectives sont des principes fondamentaux de la mécanique des sols (théorie de Terzaghi).

Formule(s)

Les formules à utiliser sont :

Contrainte totale

\sigma_v = z \cdot \gamma_{\text{sat}}

Pression interstitielle (nappe à la surface)

u_0 = z \cdot \gamma_w

Contrainte effective

\sigma'_{\text{v0}} = \sigma_v - u_0 = z \cdot (\gamma_{\text{sat}} - \gamma_w) = z \cdot \gamma'

Hypothèses

On suppose que le sol est homogène et que la nappe phréatique est statique.

Sol homogène sur 10 m d'épaisseur.
Nappe phréatique à la surface.

Donnée(s)

Nous prenons les données du sol au point de calcul :

Paramètre	Symbole	Valeur	Unité
Profondeur de calcul	z	5,0	m
Poids volumique saturé	\(\gamma_{\text{sat}}\)	18	kN/m³
Poids volumique eau	\(\gamma_{w}\)	10	kN/m³

Astuces

Le terme \( (\gamma_{\text{sat}} - \gamma_w) \) est appelé le poids volumique déjaugé, noté \(\gamma'\). C'est un raccourci très utile pour calculer directement la contrainte effective sous l'eau. Ici, \(\gamma' = 18 - 10 = 8 \, \text{kN/m³}\).

Schéma (Avant les calculs)

On se place au milieu de la couche d'argile, à z=5m sous la surface.

Point de Calcul Initial

Calcul(s)

Étape 1 : Contrainte totale

\begin{aligned} \sigma_v &= z \cdot \gamma_{\text{sat}} \\ &= 5,0 \, \text{m} \times 18 \, \text{kN/m}^3 \\ &= 90 \, \text{kPa} \end{aligned}

Étape 2 : Pression interstitielle

\begin{aligned} u_0 &= z \cdot \gamma_w \\ &= 5,0 \, \text{m} \times 10 \, \text{kN/m}^3 \\ &= 50 \, \text{kPa} \end{aligned}

Étape 3 : Contrainte effective initiale

\begin{aligned} \sigma'_{\text{v0}} &= \sigma_v - u_0 \\ &= 90 \, \text{kPa} - 50 \, \text{kPa} \\ &= 40 \, \text{kPa} \end{aligned}

(Alternative avec \(\gamma'\))

\begin{aligned} \sigma'_{\text{v0}} &= z \cdot \gamma' \\ &= 5,0 \, \text{m} \times (18 - 10) \, \text{kN/m}^3 \\ &= 5,0 \times 8 \\ &= 40 \, \text{kPa} \end{aligned}

Schéma (Après les calculs)

Diagramme des Contraintes Initiales

Réflexions

La contrainte effective initiale de 40 kPa représente la "pré-charge" naturelle du sol au point de calcul avant tous travaux. C'est notre état de référence.

Points de vigilance

Ne pas confondre poids volumique total (\(\gamma_{\text{sat}}\)) et déjaugé (\(\gamma'\)). Utiliser \(\gamma_{\text{sat}}\) pour la contrainte totale, mais \(\gamma'\) (ou \(\sigma_v - u_0\)) pour la contrainte effective.

Points à retenir

Points clés Q1 :

Contrainte effective = Contrainte totale - Pression interstitielle.
Calcul des contraintes dans un sol saturé avec nappe à la surface.

Le saviez-vous ?

Le concept de contrainte effective a été introduit par Karl von Terzaghi en 1923, révolutionnant la mécanique des sols et permettant de comprendre des phénomènes comme la consolidation et la liquéfaction.

FAQ

Questions fréquentes sur ce calcul.

Résultat Final

Les contraintes initiales au milieu de la couche d'argile sont : \( \sigma_v = 90 \, \text{kPa} \), \( u_0 = 50 \, \text{kPa} \), et \( \sigma'_{\text{v0}} = 40 \, \text{kPa} \).

A vous de jouer

En utilisant la même logique, quelle serait la contrainte effective initiale \( \sigma'_{\text{v0}} \) à la base de la couche d'argile (\(z=10\,\text{m}\)) ?

Mini Fiche Mémo

Synthèse Q1 : Contraintes Initiales

\(\sigma_v = z \cdot \gamma_{\text{sat}}\)
\(u_0 = z \cdot \gamma_w\)
\(\sigma'_{\text{v0}} = \sigma_v - u_0\) ou \(z \cdot \gamma'\)

Question 2 : Calculer la contrainte additionnelle (\( \Delta\sigma' \))

Principe

La contrainte additionnelle (\( \Delta\sigma' \)) est la nouvelle charge appliquée à la surface du sol. Dans ce cas, c'est simplement le poids du remblai. L'exercice suppose que cette charge est uniforme sur toute l'épaisseur de l'argile (une simplification pour les remblais larges).

Mini-Cours

Pour un chargement uniforme et de grande étendue (comme un large remblai), l'augmentation de contrainte verticale en profondeur peut être considérée comme égale à la charge appliquée en surface.

Remarque Pédagogique

Cette simplification est raisonnable ici. Pour des charges plus ponctuelles (fondations), la contrainte additionnelle diminuerait avec la profondeur (diffusion des contraintes).

Normes

Ce calcul relève des bases de la mécanique des sols et de l'évaluation des charges appliquées.

Formule(s)

Contrainte due au remblai

\Delta\sigma' = H_{\text{remb}} \cdot \gamma_{\text{remb}}

Hypothèses

On suppose que le remblai applique une charge uniforme et que sa largeur est suffisamment grande pour que la contrainte induite soit constante en profondeur (modèle 1D).

Charge uniforme.
Diffusion 1D des contraintes.

Donnée(s)

Paramètre	Symbole	Valeur	Unité
Hauteur remblai	\(H_{\text{remb}}\)	8,0	m
Poids volumique remblai	\(\gamma_{\text{remb}}\)	20	kN/m³

Astuces

Vérifiez toujours les unités : \([\text{m}] \times [\text{kN/m}^3]\) donne bien des \([\text{kN/m}^2]\) ou \([\text{kPa}]\), qui est l'unité d'une contrainte.

Schéma (Avant les calculs)

Le remblai ajoute une charge sur la surface initiale du sol.

Charge du Remblai

Calcul(s)

Application de la formule

\begin{aligned} \Delta\sigma' &= H_{\text{remb}} \cdot \gamma_{\text{remb}} \\ &= 8,0 \, \text{m} \times 20 \, \text{kN/m}^3 \\ &= 160 \, \text{kPa} \end{aligned}

Schéma (Après les calculs)

Ajout de la Contrainte Additionnelle

Réflexions

Cette charge de 160 kPa est très importante. Elle est 4 fois supérieure à la contrainte effective initiale au milieu de la couche (40 kPa). On peut donc s'attendre à un tassement significatif.

Points de vigilance

Ne pas oublier que cette contrainte s'ajoute à la contrainte *effective* initiale. Elle ne s'ajoute pas directement à la contrainte totale.

Points à retenir

Points clés Q2 :

La charge d'un remblai large est \( H_{\text{remb}} \cdot \gamma_{\text{remb}} \).
Cette charge représente l'augmentation de contrainte effective \( \Delta\sigma' \) dans le sol sous-jacent (en 1D).

Le saviez-vous ?

Pour des charges non uniformes ou non infinies, on utilise des abaques (comme ceux de Fadum ou Newmark) ou des logiciels pour calculer la distribution de \( \Delta\sigma' \) en profondeur et latéralement.

FAQ

...

Résultat Final

La contrainte additionnelle induite par le remblai est \( \Delta\sigma' = 160 \, \text{kPa} \).

A vous de jouer

Que deviendrait \( \Delta\sigma' \) si le remblai ne faisait que \(6 \, \text{m}\) de haut ?

Mini Fiche Mémo

Synthèse Q2 : Contrainte Additionnelle

\(\Delta\sigma' = H_{\text{remb}} \cdot \gamma_{\text{remb}}\) (pour remblai large)

Question 3 : Calculer la contrainte effective finale (\( \sigma'_{\text{vf}} \))

Principe

La contrainte effective finale est la contrainte que le sol supportera "à la fin", une fois que toute l'eau aura été expulsée et que la consolidation sera terminée. C'est la somme de la contrainte initiale et de la charge ajoutée.

Mini-Cours

À la fin de la consolidation, la surpression interstitielle générée par la charge (\(\Delta u\)) s'est dissipée (\(\Delta u \rightarrow 0\)). Toute la charge additionnelle est alors reportée sur le squelette solide, augmentant la contrainte effective.

Remarque Pédagogique

Cette contrainte finale est cruciale car c'est elle qui détermine l'état d'équilibre final du sol et l'amplitude totale du tassement.

Normes

Basé sur le principe de la contrainte effective.

Formule(s)

Contrainte finale

\sigma'_{\text{vf}} = \sigma'_{\text{v0}} + \Delta\sigma'

Hypothèses

On suppose que la consolidation est complète.

Donnée(s)

Paramètre	Symbole	Valeur	Unité
Contrainte initiale	\(\sigma'_{\text{v0}}\)	40	kPa
Contrainte additionnelle	\(\Delta\sigma'\)	160	kPa

Astuces

C'est une simple addition, mais assurez-vous d'utiliser les bonnes valeurs calculées aux étapes précédentes.

Schéma (Avant les calculs)

Visualisation de l'ajout des contraintes.

Contrainte Initiale + Additionnelle

Calcul(s)

Application de la formule

\begin{aligned} \sigma'_{\text{vf}} &= \sigma'_{\text{v0}} + \Delta\sigma' \\ &= 40 \, \text{kPa} + 160 \, \text{kPa} \\ &= 200 \, \text{kPa} \end{aligned}

Schéma (Après les calculs)

Diagramme des Contraintes Finales

Réflexions

La contrainte effective au milieu de la couche a été multipliée par 5 (\(200/40 = 5\)). C'est ce rapport élevé qui va causer un tassement important, car le tassement dépend du logarithme de ce rapport.

Points de vigilance

S'assurer que \(\sigma'_{\text{v0}}\) et \(\Delta\sigma'\) correspondent bien au même point de calcul (ici, le milieu de la couche).

Points à retenir

Points clés Q3 :

Contrainte effective finale = initiale + additionnelle.
Représente l'état d'équilibre après dissipation des surpressions interstitielles.

Le saviez-vous ?

Le temps nécessaire pour atteindre cette contrainte finale (et donc le tassement final) dépend de la perméabilité de l'argile et de la distance que l'eau doit parcourir pour s'échapper (chemin de drainage). Cela peut prendre des décennies pour des couches épaisses et peu perméables.

FAQ

...

Résultat Final

La contrainte effective finale au milieu de la couche d'argile sera \( \sigma'_{\text{vf}} = 200 \, \text{kPa} \).

A vous de jouer

Si la contrainte initiale \(\sigma'_{\text{v0}}\) était de \(60 \, \text{kPa}\) et la contrainte additionnelle \(\Delta\sigma'\) de \(100 \, \text{kPa}\), que vaudrait \(\sigma'_{\text{vf}}\) ?

Mini Fiche Mémo

Synthèse Q3 : Contrainte Finale

\(\sigma'_{\text{vf}} = \sigma'_{\text{v0}} + \Delta\sigma'\)

Question 4 : Estimer le tassement total (\( S_f \))

Principe

Maintenant que nous avons toutes les composantes (paramètres du sol, contraintes initiale et finale), nous pouvons appliquer la formule du tassement oedométrique pour un sol normalement consolidé.

Mini-Cours

La formule \( S_f = \frac{C_c}{1 + e_0} \cdot H_{\text{sol}} \cdot \log_{10} \left( \frac{\sigma'_{\text{vf}}}{\sigma'_{\text{v0}}} \right) \) relie la déformation volumique (via \(C_c\) et \(e_0\)) à la variation relative de contrainte effective (via le logarithme du rapport). Multiplier par l'épaisseur \(H_{\text{sol}}\) donne le tassement total.

Remarque Pédagogique

Cette formule est l'une des plus importantes en géotechnique pour l'estimation des tassements primaires.

Normes

Basé sur la théorie de la consolidation de Terzaghi et les essais oedométriques en laboratoire qui permettent de déterminer \(C_c\) et \(e_0\).

Formule(s)

Tassement Oedométrique (NC)

S_f = \frac{C_c}{1 + e_0} \cdot H_{\text{sol}} \cdot \log_{10} \left( \frac{\sigma'_{\text{vf}}}{\sigma'_{\text{v0}}} \right)

Hypothèses

On maintient les hypothèses précédentes et on ajoute :

Le sol est normalement consolidé.
La consolidation est unidimensionnelle (pas de déformation latérale).
Les paramètres \(C_c\) et \(e_0\) sont constants dans la plage de contrainte considérée.

Donnée(s)

Paramètre	Symbole	Valeur	Unité
Indice de compression	\(C_c\)	0,45	-
Indice des vides initial	\(e_0\)	1,20	-
Épaisseur de la couche	\(H_{\text{sol}}\)	10,0	m
Contrainte finale	\(\sigma'_{\text{vf}}\)	200	kPa
Contrainte initiale	\(\sigma'_{\text{v0}}\)	40	kPa

Astuces

Le terme \(\frac{C_c}{1 + e_0}\) est parfois appelé Indice de Compressibilité Modifié. Calculez-le séparément pour simplifier l'expression finale.

Schéma (Avant les calculs)

Le tassement est l'affaissement vertical de la couche d'argile.

Visualisation du Tassement

Points de vigilance

Assurez-vous que les contraintes \(\sigma'_{\text{vf}}\) et \(\sigma'_{\text{v0}}\) sont dans la même unité (ici, kPa), car elles sont dans un rapport. L'épaisseur \(H_{\text{sol}}\) donnera l'unité du tassement final (ici, en mètres). Attention à bien utiliser le logarithme en base 10 (\(\log_{10}\)) et non le logarithme népérien (\(\ln\)).

Calcul(s)

Étape 1 : Calcul du rapport de compressibilité

\begin{aligned} \frac{C_c}{1 + e_0} &= \frac{0,45}{1 + 1,20} \\ &= \frac{0,45}{2,20} \\ &\approx 0,2045 \end{aligned}

Étape 2 : Calcul du terme logarithmique

\begin{aligned} \log_{10} \left( \frac{\sigma'_{\text{vf}}}{\sigma'_{\text{v0}}} \right) &= \log_{10} \left( \frac{200}{40} \right) \\ &= \log_{10}(5) \\ &\approx 0,699 \end{aligned}

Étape 3 : Calcul final du tassement

\begin{aligned} S_f &= \frac{C_c}{1 + e_0} \cdot H_{\text{sol}} \cdot \log_{10} \left( \frac{\sigma'_{\text{vf}}}{\sigma'_{\text{v0}}} \right) \\ &= (0,2045) \cdot (10,0 \, \text{m}) \cdot (0,699) \\ &\approx 1,43 \, \text{m} \end{aligned}

Schéma (Après les calculs)

Illustration du Tassement Final

Réflexions

Un tassement de \(1,43 \, \text{m} (143 \, \text{cm})\) est extrêmement important. Un tel affaissement rendrait une route impraticable et causerait des dommages majeurs à toute structure rigide fondée dessus.

Points à retenir

Points clés Q4 :

Formule du tassement oedométrique pour sol NC.
Le tassement dépend de la compressibilité (\(C_c, e_0\)), de l'épaisseur (\(H_{\text{sol}}\)) et de l'augmentation relative de contrainte (\(\log(\sigma'_{\text{vf}}/\sigma'_{\text{v0}})\)).

Le saviez-vous ?

La Tour de Pise penche à cause d'un tassement différentiel important dans les couches d'argile sous ses fondations. Un côté a tassé beaucoup plus que l'autre.

FAQ

...

Résultat Final

Le tassement final estimé de la couche d'argile est \( S_f \approx 1,43 \, \text{m} \).

A vous de jouer

Recalculez le tassement (en cm) si le sol était de meilleure qualité, avec un indice de compression \( C_c = 0,30 \). (Tous les autres paramètres restent inchangés).

Mini Fiche Mémo

Synthèse Q4 : Calcul Tassement

\( S_f = \frac{C_c}{1 + e_0} \cdot H_{\text{sol}} \cdot \log_{10} \left( \frac{\sigma'_{\text{vf}}}{\sigma'_{\text{v0}}} \right) \) (Sol NC)

Question 5 : Acceptabilité du tassement et solutions

Principe

Comparer le tassement calculé aux valeurs généralement admises pour ce type d'ouvrage (une route) et envisager des solutions si nécessaire.

Réflexions

Le tassement calculé est de \(S_f \approx 1,43 \, \text{m}\). Pour une route, les tassements acceptables sont de l'ordre de quelques centimètres seulement. Un tassement de plus d'un mètre est inacceptable.

Cela entraînerait des déformations importantes de la chaussée [Image d'une route déformée par le tassement], des problèmes de drainage et des risques pour la sécurité.

Points à retenir

Solutions Techniques Courantes :

Face à un tassement excessif, il faut traiter le sol avant de construire. Voici quelques options :

Pré-chargement (+ Drains Verticaux) : Appliquer une charge temporaire pour "forcer" le tassement avant les travaux, souvent accéléré par des drains qui évacuent l'eau plus vite.
Renforcement (Inclusions, Colonnes) : Transférer la charge du remblai vers des couches de sol plus résistantes en profondeur.
Allègement : Utiliser des matériaux plus légers (ex: polystyrène) pour le remblai afin de réduire la charge appliquée.
Substitution : Remplacer le mauvais sol par un meilleur matériau (souvent coûteux et peu pratique pour de grandes épaisseurs).

Le saviez-vous ?

Le choix de la solution dépend du coût, du délai disponible, de l'environnement et de l'ampleur du tassement à réduire.

Résultat Final

Le tassement calculé (\( \approx 1,43 \, \text{m} \)) est largement supérieur aux limites admissibles pour une route. Des mesures correctives (traitement ou renforcement du sol) sont indispensables avant la construction.

Mini Fiche Mémo

Synthèse Q5 : Analyse et Solutions

Comparer \(S_f\) calculé aux tassements admissibles.
Connaître les solutions : pré-chargement, drains, renforcement, allègement, substitution.

Outil Interactif : Simulateur de Tassement

Utilisez cet outil pour voir comment la hauteur du remblai et la compressibilité du sol (\(C_c\)) influencent le tassement final. (Les autres paramètres sont fixés à \(H_{\text{sol}}=10\,\text{m}\), \(e_0=1,20\), \(\sigma'_{\text{v0}}=40\,\text{kPa}\)).

Paramètres d'Entrée

Hauteur du remblai (\(H_{\text{remb}}\)) (m) 8.0 m

Indice de compression (\(C_c\)) (-) 0.45 -

Résultats Clés

Contrainte additionnelle (\( \Delta\sigma' \)) - kPa

Tassement final (\( S_f \)) - cm

Glossaire

Tassement: Affaissement vertical d'un sol sous l'effet d'une charge.
Consolidation: Processus lent d'expulsion de l'eau des pores d'un sol saturé (comme l'argile), entraînant une réduction de volume (tassement).
Contrainte Effective (\(\sigma'\)): Pression s'exerçant sur le squelette solide du sol (\(\sigma' = \sigma - u\)). C'est elle qui gouverne la résistance et la déformation du sol.
Indice de Compression (\(C_c\)): Paramètre de laboratoire mesurant la compressibilité d'un sol. C'est la pente de la courbe de compressibilité dans un diagramme \(e - \log(\sigma')\).
Sol Normalement Consolidé (NC): Un sol qui n'a jamais subi, dans son histoire géologique, une contrainte effective supérieure à sa contrainte effective actuelle.
Pression Interstitielle (u): Pression de l'eau dans les pores du sol.
Indice des Vides (e): Rapport du volume des vides sur le volume des grains solides dans un échantillon de sol (\(e = V_v / V_s\)).
Poids Volumique Déjaugé (\(\gamma'\)): Poids volumique effectif du sol sous l'eau (\(\gamma' = \gamma_{\text{sat}} - \gamma_w\)).

Calcul du Tassement d’un Remblai sur Sol Compressible

Objectifs Pédagogiques

Données de l'étude : Remblai sur Argile

Fiche Technique

Schéma du Remblai sur Sol Compressible

Questions à traiter

Les bases du Tassement par Consolidation

Correction : Calcul du Tassement d'un Remblai sur Sol Compressible

Question 1 : Calculer la contrainte effective initiale (\( \sigma'_{\text{v0}} \))

Principe

Mini-Cours

Remarque Pédagogique

Normes

Formule(s)

Hypothèses

Donnée(s)

Astuces

Schéma (Avant les calculs)

Point de Calcul Initial

Calcul(s)

Schéma (Après les calculs)

Diagramme des Contraintes Initiales

Réflexions

Points de vigilance

Points à retenir

Le saviez-vous ?

FAQ

Résultat Final

A vous de jouer

Mini Fiche Mémo

Question 2 : Calculer la contrainte additionnelle (\( \Delta\sigma' \))

Principe

Mini-Cours

Remarque Pédagogique

Normes

Formule(s)

Hypothèses

Donnée(s)

Astuces

Schéma (Avant les calculs)

Charge du Remblai

Calcul(s)

Schéma (Après les calculs)

Ajout de la Contrainte Additionnelle

Réflexions

Points de vigilance

Points à retenir

Le saviez-vous ?

FAQ

Résultat Final

A vous de jouer

Mini Fiche Mémo

Question 3 : Calculer la contrainte effective finale (\( \sigma'_{\text{vf}} \))

Principe

Mini-Cours

Remarque Pédagogique

Normes

Formule(s)

Hypothèses

Donnée(s)

Astuces

Schéma (Avant les calculs)

Contrainte Initiale + Additionnelle

Calcul(s)

Schéma (Après les calculs)

Diagramme des Contraintes Finales

Réflexions

Points de vigilance

Points à retenir

Le saviez-vous ?

FAQ

Résultat Final

A vous de jouer

Mini Fiche Mémo

Question 4 : Estimer le tassement total (\( S_f \))

Principe

Mini-Cours

Remarque Pédagogique

Normes

Formule(s)